Situaciones de aprendizaje

Descarga los modelos a continuación, o bien accede a la versión editable

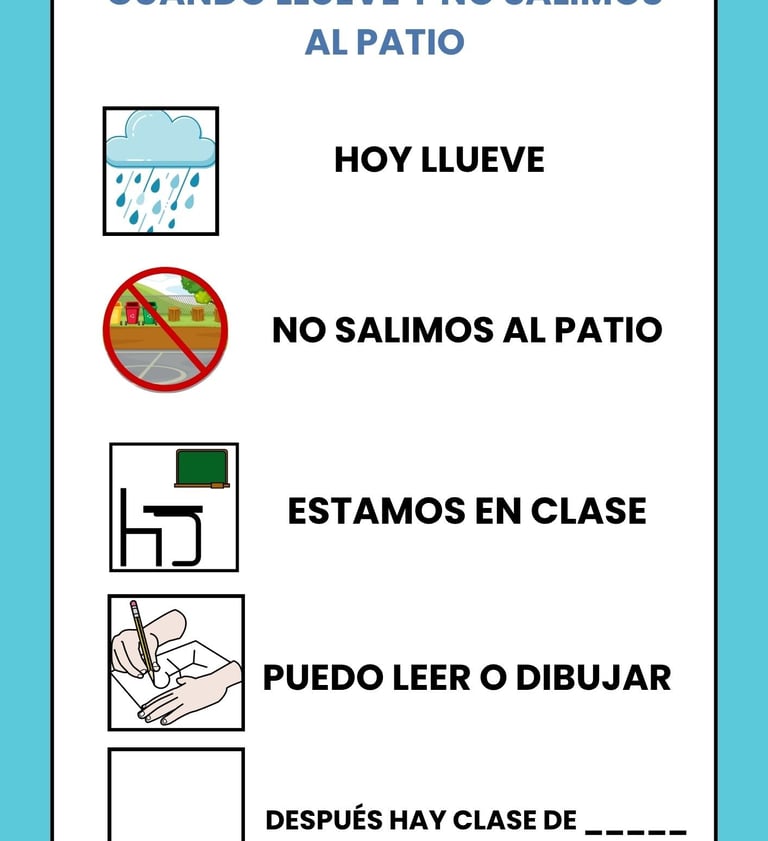
Historias sociales para imprevistos en el aula: apoyos visuales para alumnado TEA

Cuaderno con historias sociales para ayudar al alumnado TEA a entender y gestionar cambios inesperados en la rutina escolar —como lluvia sin patio o excursiones canceladas— mediante apoyos visuales claros y calmados.

Plantilla descargable y editable para elaborar SdA

Accede a la plantilla editable en Canva aquí

CALCULAR EL m.c.m y el M.C.D. CON EL DIAGRAMA DE VENN

Una estrategia fácil, práctica y que realmente funciona

En 5.º y 6.º de Primaria, muchos alumnos empiezan a mostrar dificultad para diferenciar el Máximo Común Divisor (MCD) y el Mínimo Común Múltiplo (MCM). A menudo recuerdan la definición, pero no saben identificar qué cálculo corresponde a cada uno.
El diagrama de Venn es una herramienta visual muy efectiva que ayuda a organizar factores y a comprender qué elementos son comunes y cuáles no. Es sencilla, manipulativa y perfecta para trabajar paso a paso en el aula.

Paso 1: Descomposición en factores primos

Antes de llegar al diagrama, el alumnado debe descomponer cada número en sus factores primos.
Trabajamos con ejemplos simples como 12 y 30 para que interioricen la técnica:

• 12 = 2 × 2 × 3

• 30 = 2 × 3 × 5

Este paso puede reforzarse con material manipulativo como tarjetas de números, bloques o listas de primos para favorecer la autonomía.

Paso 2: Construir el diagrama de Venn

Dibujamos dos circunferencias que se superponen.
En cada una irá un número, y en la zona central colocaremos los factores comunes.

Paso 3: Colocar los factores primos

El objetivo es repartir los factores según su pertenencia:

• Los factores comunes se colocan en la zona central.
  Ejemplo: el 2 y el 3 aparecen en ambos números, así que se sitúan en la intersección.

• Los factores no comunes se colocan en las partes externas del diagrama:

  • Para 12 quedará un 2 adicional.

  • Para 30, el 5.

Este momento es clave: permite al alumnado ver la diferencia entre lo que comparten los números y lo que no.

Paso 4: Calcular el MCD

El MCD se obtiene multiplicando únicamente los factores que están dentro de la intersección.

En el ejemplo:
MCD = 2 × 3 = 6

Explícaselo así a tus alumnos: “El MCD siempre se forma con lo que los dos números comparten”.

Paso 5: Calcular el MCM

El MCM se obtiene multiplicando todos los factores del diagrama, es decir, los comunes y los no comunes, pero cada uno una sola vez.

En el ejemplo:
MCM = 2 × 3 × 2 × 5 = 60

Una explicación clara para el aula sería:
“El MCM significa unirlo todo: lo que comparten y lo que no comparten los números”.

Por qué funciona tan bien esta estrategia

• Es visual: el alumnado asocia rápidamente “lo común” y “lo propio” gracias al esquema.

• Es manipulativa: permite trabajar con tarjetas, imanes o materiales físicos.

• Favorece la comprensión profunda, no solo la memorización.

• Reduce errores típicos como mezclar los conceptos de múltiplo y divisor.

Sugerencias para docentes

• Utiliza colores diferentes para los factores comunes y no comunes.

• Pide a los alumnos que expliquen el proceso a un compañero (técnica peer teaching).

• Presenta primero ejemplos pequeños para que consoliden la técnica antes de aumentar la dificulta tu texto aquí...

SELLA: una estrategia visual para enseñar las palabras agudas, llanas, esdrújulas y sobreesdrújulas

Enseñar las reglas de acentuación suele ser un reto en el aula. Muchos alumnos memorizan las normas sin comprender realmente cómo se aplican. La estrategia SELLA ofrece una forma visual, manipulativa y estructurada de interiorizar las reglas ortográficas relacionadas con la acentuación.

¿Qué es la estrategia SELLA?

SELLA es un acrónimo que agrupa los cuatro tipos de palabras según la posición de la sílaba tónica:

• S → Sobreesdrújulas: siempre llevan tilde.

• E → Esdrújulas: siempre llevan tilde.

• LL → Llanas: llevan tilde solo si terminan en consonante distinta de “n” o “s”.

• A → Agudas: llevan tilde si terminan en vocal, “n” o “s”.

Este esquema permite al alumnado visualizar la jerarquía de las palabras de manera ordenada y facilita la comprensión de cuándo y por qué se coloca la tilde.

Instrucciones paso a paso

1. Separar en sílabas.
   Se comienza dividiendo la palabra en sus sílabas correspondientes. Este paso ayuda a desarrollar la conciencia fonológica y la segmentación silábica.

2. Colocar una sílaba en cada columna (S, E, LL, A).
   Si la palabra tiene tres sílabas, se empieza en la columna “E” (esdrújula). Si tiene más, en la “S” (sobreesdrújula). Así, se puede observar visualmente dónde recae la sílaba tónica.

3. Rodear la sílaba tónica.
   Se marca la sílaba que lleva la mayor fuerza de voz. Este paso es clave para identificar correctamente el tipo de palabra.

4. Identificar el tipo de palabra y aplicar la regla de acentuación.
   Finalmente, se analiza la última letra de la palabra y se aplica la norma ortográfica correspondiente para decidir si lleva o no tilde.

Ejemplo práctico

En la plantilla de la imagen se presenta el ejemplo “estuche”:

• Se separa en sílabas: es-tu-che.

• Se colocan las sílabas en las columnas correspondientes.

• Se rodea la sílaba tónica (tu).

• Se identifica como palabra llana, porque termina en vocal y no lleva tilde.

De este modo, el alumnado comprende visualmente el proceso de acentuación sin depender únicamente de la memorización.

Beneficios de la técnica SELLA

• Facilita un aprendizaje significativo de las reglas de acentuación.

• Refuerza la conciencia silábica y fonológica.

• Ayuda a diferenciar los tipos de palabras de forma visual y estructurada.

• Promueve la autonomía del alumnado al analizar palabras nuevas.

• Se adapta fácilmente a diferentes niveles de Primaria.

Conclusión

La estrategia SELLA convierte el estudio de la acentuación en un proceso lógico, visual y comprensible. A través de pasos sencillos y de un apoyo gráfico claro, los estudiantes aprenden a reconocer, clasificar y acentuar las palabras de forma autónoma y razonada, fortaleciendo así su competencia lingüística y ortográfica.

Haz click en el enlace descarga la plantilla de forma gratuita

TARJETAS DE APOYO VISUAL

ESENCIALES EN LA ENSEÑANZA

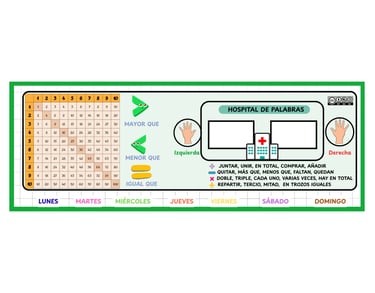
          En el aula de Primaria, especialmente cuando trabajamos con alumnado que necesita refuerzo en funciones ejecutivas, disponer de apoyos visuales concretos y accesibles marca una diferencia real en su rendimiento diario. Las tarjetas de apoyo que utilizamos en la mesa del alumnado —como las que se presentan en este apartado— no son un simple recurso decorativo: son una herramienta pedagógica clave para entrenar la memoria operativa, favorecer la autonomía y reducir la carga cognitiva durante las tareas escolares.

Estas tarjetas incluyen elementos esenciales:

• Abecedario completo en mayúsculas y minúsculas, para apoyar la recuperación rápida de grafías.

• Signos matemáticos básicos (mayor que, menor que, igual que).

• Días de la semana, que facilitan la orientación temporal.

• Banco de palabras clave para la resolución de problemas matemáticos, lo que ayuda al alumnado a identificar operaciones sin saturar su memoria.

• Registros emocionales sencillos, que favorecen la autorregulación.

Desde una perspectiva pedagógica, estos apoyos funcionan como “andamios cognitivos” que permiten que el alumnado mantenga activa la información relevante mientras realiza una tarea. En alumnos con dificultades de memoria operativa, atención sostenida o discalculia, esta visualización inmediata evita que tengan que “ir y volver mentalmente” a información básica, permitiendo que centren sus recursos en el proceso principal: leer, escribir, resolver un problema o seguir una secuencia de instrucciones.

Beneficios pedagógicos de este tipo de tarjetas

1. Descarga cognitiva: al tener la información relevante a la vista, el alumnado reduce el esfuerzo mental dedicado a recuperar datos simples, mejorando la precisión y la velocidad en la tarea.

2. Incremento de la autonomía: evitan interrupciones constantes (“¿cómo era el símbolo de menor?”, “¿qué día va después del martes?”) y favorecen hábitos de autoconsulta.

3. Apoyo constante a la memoria operativa: el alumnado mantiene en mente la información esencial sin sobrecargarla, pudiendo manipularla y aplicarla correctamente.

4. Facilitan la consolidación: la exposición diaria a estos apoyos favorece la automatización progresiva de letras, signos matemáticos y vocabulario clave.

5. Inclusión real en el aula: permiten que estudiantes con necesidades de apoyo específico trabajen al mismo ritmo que el grupo manteniendo accesibles los recursos que necesitan.

Como docentes de Educación Primaria, nuestra tarea no es únicamente enseñar contenidos, sino crear las condiciones para que todo el alumnado pueda procesarlos y aplicarlos. Estas tarjetas, sencillas pero potentes, se convierten así en un recurso imprescindible para que nuestros alumnos desarrollen mayor seguridad, precisión y autonomía en sus aprendizajes diarios.